اعداد صحیح برای شمارش مناسب هستند، اما گاهی اوقات ما نیاز داریم که اعداد بسیار بزرگ یا اعدادی با جزء کسری را ذخیره کنیم. اعداد اعشاری یا همان اعداد حقیقی برای ارزشگذاری عبارتهایی كه نیازمند دقت بیشتری هستند، استفاده میشوند. برخلاف اعداد صحیح که به آسانی میتوان آنها را به مقادیر دودویی (binary) تبدیل کرده و در سیستمهای کامپیوتری استفاده نمود، برای اعداد اعشاری چالش بزرگی پیش رو است تا علاوه بر تبدیل بهینهی اعداد اعشاری به مقادیر دودویی، دامنهی بزرگی از اعداد را هم شامل شود و همچنین دارای دقت و سرعت پردازش بالایی باشد.
در علوم کامپیوتر از اصطلاح ممیز شناور (floating point) به عنوان روشی برای نمایش اعداد اعشاری به طوری که محدودهای وسیع از مقادیر را بپذیرند، استفاده میشود. اصطلاح “ممیز شناور” به این واقعیت اشاره دارد که علامت ممیز اعشار میتواند “شناور” باشد. یعنی میتواند تعداد متغیری از ارقام، قبل و بعد از علامت ممیز اعشار داشته باشد.
در گذشته کامپیوترهای گوناگون روشهای متفاوتی در پردازش مقادیر ممیز شناور داشتند که این موضوع باعث میشد برنامهها بر روی کامپیوترهای مختلف جوابهای یکسانی را در خروجی نمایش ندهند. به همین منظور در سال 1985 با تلاش گروهی متشکل از ریاضیدانان، دانشمندان علوم کامپیوتر و شرکتهای تولید سختافزار به سرپرستی William Kahan از دانشگاه کالیفرنیا، استانداردی برای مقادیر ممیز شناور تحت عنوان IEEE754 به سازندگان سختافزارها عرضه شد. با مطرح شدن استاندارد IEEE754 واگرایی شیوههای به کار رفته برای نمایش مقادیر ممیز شناور کاهش یافت و بدین ترتیب برنامههای نوشته شده برای مقاصد علمی قابل حمل شدند. بسیاری از کامپیوترهای امروزی برای استفاده از مقادیر ممیز شناور از این استاندارد پیروی میکنند.
طبق این استاندارد روش نمایش و ذخیرهسازی متغیرهایی از نوع داده ممیز شناور بسیار شبیه به چگونگی نوشتن اعداد با نماد علمی (scientific notation) میباشد. نماد علمی یک روش معمول خلاصهنویسی در مورد اعداد خیلی بزرگ یا خیلی کوچک میباشد. در نگاه اول شاید نماد علمی کمی پیچیده به نظر برسد، اما اگر فهم درستی از نماد علمی داشته باشید، به شما کمک میکند تا درک کنید که نوع دادهای ممیز شناور چگونه کار میکند، و مهمتر از آن دارای چه محدودیتهایی میباشد.
نماد علمی
در نماد علمی هر عددی میتواند، به صورت حاصلضرب دو عدد به شکل:
$$
significand * base^{exponent}
$$
نوشته شود که در آن base پایه عددی است و نما یا توان (exponent) یک عدد صحیح مثبت یا منفی، و ضریب علمی (significand) یک عدد حقیقی که در مبنای 10 بزرگتر یا مساوی 1 و کوچکتر از 10 است میباشد. هر چقدر تعداد ارقام در قسمت بعد از اعشار ضریب علمی بیشتر باشد، عدد شما دقیقتر میباشد.
برای مثال در نماد علمی زیر قسمت 1.2 ضریب علمی میباشد و عدد 4 توان میباشد. این عدد به عدد 12000 ارزیابی میگردد.
$$
1.2 * 10^{4}
$$
به عنوان مثال جرم زمین را در نظر بگیرید. اگر بخواهیم جرم زمین را در مبنای دهدهی بنویسیم عددی برابر 5973600000000000000000000 کیلوگرم میشود. این یک عدد بسیار بزرگ است. همچنین خواندن آن نیز خیلی سخت است (آیا 19 صفر دارد یا 20 صفر؟). اگر جرم زمین را بخواهیم با نماد علمی بنویسیم، خواهیم داشت:
$$
5.9736 * 10^{24} (kg)
$$
همانطور که میبینید، خواندن نماد علمی آن بسیار سادهتر است. همچنین نماد علمی دارای مزیت دیگری است که طی آن میتوانیم سادهتر دو عدد خیلی بزرگ یا دو عدد خیلی کوچک را با هم مقایسه کنیم. این کار تنها با مقایسه توان دو عدد صورت میپذیرد.
به طوری کلی میتوان از قواعد زیر برای تبدیل اعداد به نماد علمی استفاده کنید:
- توان شما از صفر آغاز می شود.
- ممیز را به سمت چپ ببرید به نحوی که تنها یک رقم غیر از صفر در سمت چپ و قبل از ممیز قرار بگیرد.
- هر بار که ممیز را یک رقم به سمت چپ منتقل میکنید منجر میشود تا توان شما 1 واحد افزایش پیدا کند.
- هر بار که ممیز را یک رقم به سمت راست منتقل میکنید منجر میشود تا توان شما 1 واحد کاهش پیدا کند.
- صفرهای قبل از عدد را حذف کنید.
- صفرهای بعد از عدد را تنها در صورتی حذف کنید که عدد اصلی شما دارای ممیز نباشد. در نماد علمی ترجیح داده میشود تا صفرهای بعد از اعشار نگهداری شده و حذف نگردد، چرا که آن صفرها دقت عدد مربوطه را ارائه میدهند.
برای درک بهتر به مثالهای زیر توجه کنید:
مثال 1
عدد اصلی: 42030
از آخرین رقم در سمت راست شروع کرده و ممیز را 4 رقم به سمت چپ میبریم:
$$
4.2030 * 10^{4}
$$
هیچ صفری قبل از عدد برای حذف کردن نداریم:
$$
4.2030 * 10^{4}
$$
یک صفر در آخرین رقم سمت راست داریم که حذفش میکنیم:
$$
4.203 * 10^{4}
$$
مثال 2
عدد اصلی: 0.0078900
ممیز را سه رقم به سمت راست میبریم تا اولین رقم قبل از ممیز (7) غیر از صفر باشد:
$$
0007.8900 * 10^{3}
$$
صفرهای قبل از عدد را از بین میبریم:
$$
7.8900 * 10^{3}
$$
از آنجا که عدد اصلی ما دارای ممیز میباشد، صفرهای سمت راست را حذف نمیکنیم:
$$
7.8900 * 10^{3}
$$
مثال 3
عدد اصلی: 600.410
ممیز را دو رقم به سمت چپ میبریم:
$$
6.00410 * 10^{2}
$$
صفر قبل از عدد نداریم که بخواهیم حذفش کنیم:
$$
6.00410 * 10^{2}
$$
از آنجا که عدد اصلی ما دارای ممیز میباشد، صفرهای سمت راست را حذف نمیکنیم:
$$
6.00410 * 10^{2}
$$
نماد علمی به صورت دیجیتال یا زمانی که توان به صورت بالانویس مقدور نیست معمولاً با E یا e که معادل «ضربدر ۱۰ به توانِ…» است نمایش داده میشود. به عنوان مثال میتوان جرم زمین را با نماد علمی به صورت زیر نیز نوشت:
$$
5.9736E24 (kg)
$$
نمایش مقادیر ممیز شناور در IEEE754
استاندارد IEEE754، چند قالب کلی با دقتهای مختلف از جمله دقت معمولی، دقت مضاعف و دقت مضاعف توسعهیافته برای نمایش اعداد ارائه مینماید. در این استاندارد، در دقت معمولی از 32 بیت، در دقت مضاعف از 64 بیت و در دقت مضاعف توسعهیافته از 128 بیت برای نمایش یک عدد استفاده میشود.
در روش ارائهشده در استاندارد IEEE754 برای نمایش و ذخیرهسازی انواع ممیز شناور از فرمول زیر استفاده میشود:
$$
(-1)^{sign} * normalized mantissa * base^{biased exponent}
$$
مبنا (base) در نظر گرفتهشده در استاندارد IEEE754 برابر 2 است. قالب دودویی انواع ممیز شناور نیز به ترتیب زیر است:
$$
sign| biased exponent | normalized mantissa
$$
علامت (sign) برای اعداد مثبت 0 و برای اعداد منفی 1 میباشد و از یک بیت برای نمایش آن استفاده میشود.
مقدار اعشاری نرمالشده (normalized mantissa) بخشی از یک عدد ممیز شناور است که از ارقام معنادار آن تشکیل شده است. بنابراین یک مقدار اعشاری نرمالشده عددی است که تنها یک عدد 1 در سمت چپ اعشار دارد. از آنجا همواره عدد سمت اعشار میبایست 1 باشد این عدد در فرمت ذخیرهسازی قرار داده نشده و به صورت پیشفرض در نظر گرفته میشود. در دقت ساده از 23 بیت، در دقت مضاعف از 52 بیت و در دقت مضاعف توسعهیافته از 112 بیت برای نمایش مقدار اعشاری نرمالشده استفاده میشود.
نما یا توان متعادلشده (biased exponent) یک عدد صحیح مثبت است که مقدار ثابتی به عنوان bias به آن اضافه شده است تا محدوده توان غیر منفی شود. این مقدار ثابت در دقت معمولی 127، در دقت مضاعف 1023 و در دقت مضاعف توسعهیافته 16383 است. همچنین در دقت ساده از 8 بیت، در دقت مضاعف از 11 بیت و در دقت مضاعف توسعهیافته از 15 بیت برای نمایش توان متعادلشده استفاده میشود.
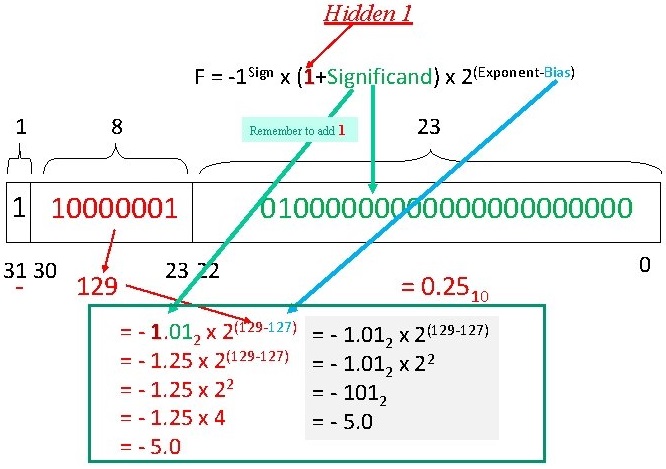
به طور مثال ما قصد داریم عدد 5.0- را در به عنوان یک مقدار ممیز شناور معمولی ذخیره کنیم.
عدد اصلی در مبنای 2: 0101-
برای تبدیل این عدد به یک مقدار اعشاری نرمالشده همانند نمایش علمی از آخرین رقم در سمت راست شروع نموده و ممیز را 2 رقم به سمت چپ میبریم تا به آخرین 1 برسیم. همچنین به ازای هر رقم یک واحد به توان اضافه میکنیم:
$$
-01.01 * 10^{2}
$$
صفر سمت چپ را نیز حذف میکنیم:
$$
-1.01 * 10^{2}
$$
مقدار ثابت bias را که در دقت معمولی برابر 127 است به توان اضافه میکنیم:
$$
-1.01 * 10^{2+127} = -1.01 * 10^{129}
$$
در عدد به دست آمده مقدار علامت برابر 1، مقدار اعشاری نرمالشده برابر 1.01 و توان متعادلشده برابر 129 است. از آنجایی که مقدار 1 سمت چپ مقدار اعشاری نرمالشده ذخیره نمیشود مقدار بیتی عدد -5.0 به صورت زیر است:
$$
0(sign)10000001(exponent)01000000000000000000000(fraction)
$$
دقت انواع ممیز شناور
از آنجایی که در مقادیر ممیز شناور دقت عدد اعشاری به تعداد بیت قسمت اعشاری محدود شده است در هنگام محاسبات مواردی پیش میآید که یک محاسبه مقداری را ایجاد میکند که نمیتواند دقیقا به وسیلهی قالب ممیز شناور ارائه شده توسط IEEE754 نمایش داده شود و سختافزار باید نتیجه را به مقداری که به درستی نمایش داده میشود، گرد کند. در استاندارد IEEE754، روش پیشفرض برای این کار این است که به نزدیکترین عدد ممکن گرد شود. به عنوان مثال مقدار 1.0 در قالب ممیز شناور به صورت زیر است: $$ 0(sign)01111111(exponent)00000000000000000000000(fraction) $$ که در فرمول IEEE754 به صورت زیر قرار می گیرد: $$ 1.00000000000000000000000(binary) × 2⁰ $$ که برابر عدد زیر در مبنای 2 است: $$ 1.00000000000000000000000 $$ کوچک ترین عددی که می توان به این عدد اضافه یا از این عدد کم کرد برابر با مقدار زیر است: $$ 0.00000000000000000000001(binary) = 0.00000011920928955078(decimal) $$ اگر عددی کوچکتر از 0.00000011920928955078 را جمع یا تفریق کنید، نتیجه تغییر نخواهد کرد زیرا نتیجه به مقدار قبلی گرد میشود. وقتی از عدد شناور معمولی استفاده میکنید این دقتی است که با عدد 1.0 دارید. در واقع در این مورد مشکل بزرگی نیست زیرا 0.00000011920928955078 برای اکثر برنامهها به اندازه کافی کوچک است. به عنوان مثالی دیگر مقدار 1000000.0 در قالب ممیز شناور به صورت زیر است: $$ 0(sign)10010010(exponent)11101000010010000000000(fraction) $$ که در فرمول IEEE754 به صورت زیر قرار میگیرد: $$ 1.11101000010010000000000(binary) × 2¹⁹ $$ که برابر عدد 11110100001001000000.0000 در مبنای 2 است: $$ 11110100001001000000.0000 $$ کوچکترین عددی که میتوان به این عدد اضافه یا از این عدد کم کرد برابر با مقدار زیر است: $$ 0.0001(binary) = 0.0625(decimal) $$ در این مورد، دقت در مقایسه با زمانی که عدد 1.0 است بسیار کمتر است که این میتواند مشکلساز باشد. به عنوان مثال اگر از نوع ممیز شناور با دقت معمولی برای نمایش زمان (ثانیه) از زمان شروع یک برنامه کاربردی استفاده شده باشد و برنامه هر 0.05 ثانیه زمان را شمارش کند، پس از 1000000.0 (یا قبل از آن)، زمان از حرکت باز میایستد!